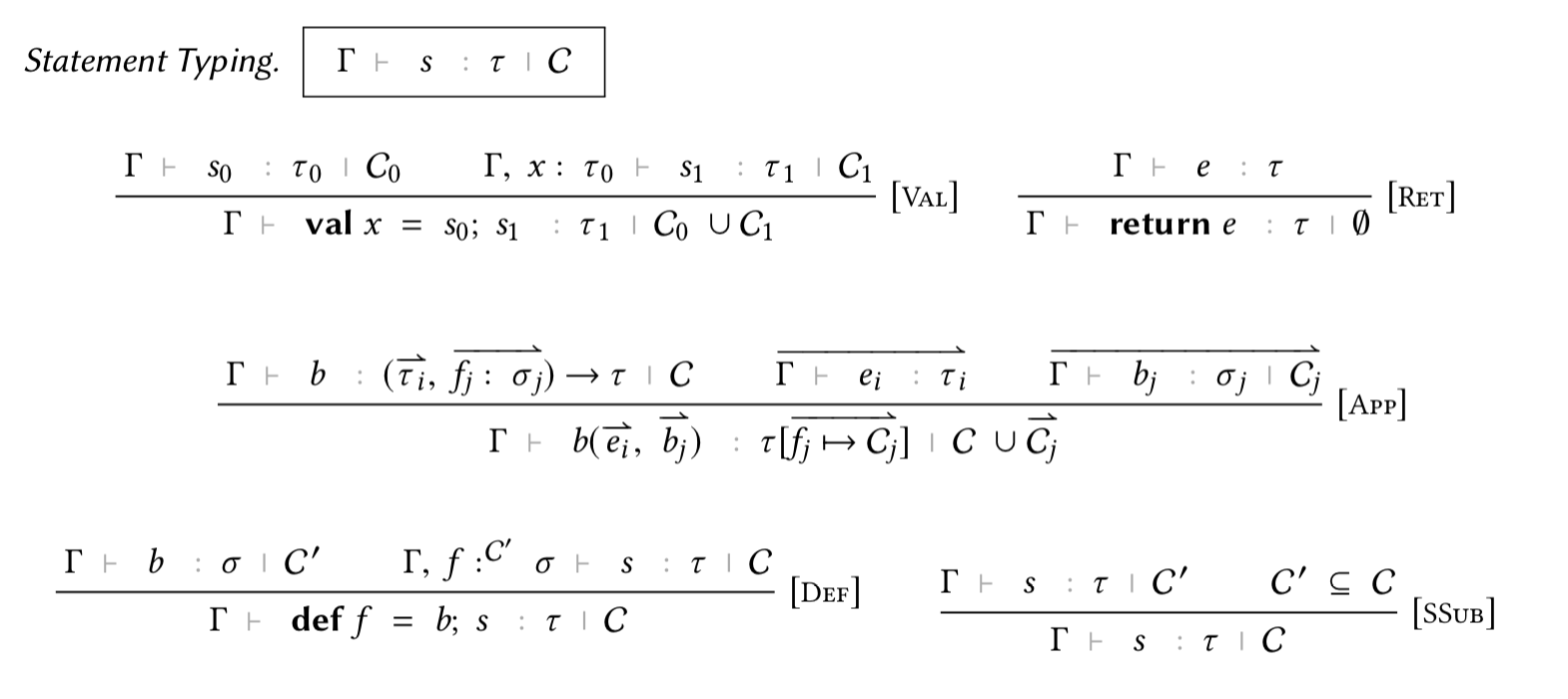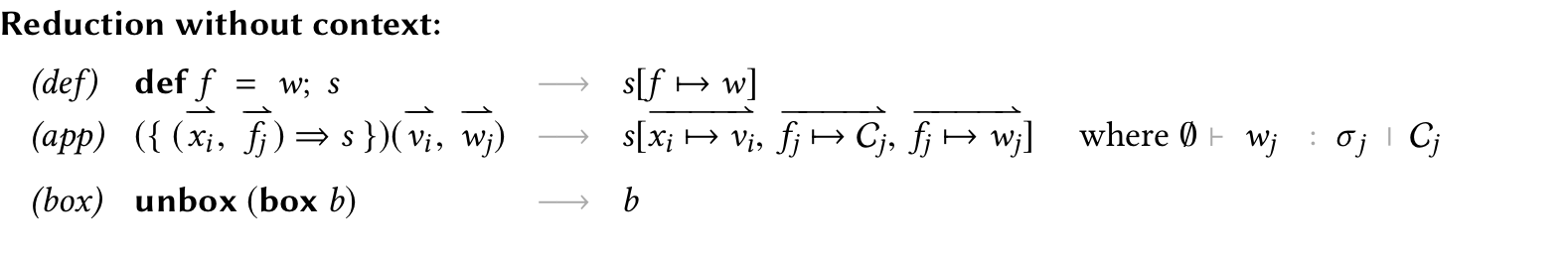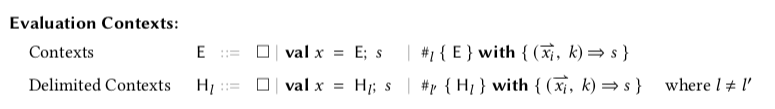Top.SystemC.Definitions
The source of this file can be found on Github.
This file contains the definitions for System C. We include snippets of the paper as images to facilitate comparison. Syntax Environments and Signatures Typing Operational Semantics The definitions here reflect the definitions in Figure 1 from the paper. Please note that we base our proofs on a locally nameless representation. Consequently there are always two kinds of variables, free variables (such as typ_fvar) and locally bound variables (such as typ_bvar). Capture sets cap are records, containing sets of free variables, sets of bound variables, and sets of labels. Here, we define the syntax of types, as defined in Figure 1 in the paper. 
Table of Contents
- Values
- Machine Redexes
- Trivial Reduction
- Stacks, Contexts, and their Typing
- Abstract Machine
- Machine Reduction
- Abstract Machine Typing
Syntax
Syntax of Types

Value Types
Inductive vtyp : Type :=
| typ_base : vtyp (* base types *)
| typ_capt : btyp → cap → vtyp (* boxed block types *)
| typ_fvar : atom → vtyp (* (free) value-type variables *)
| typ_bvar : nat → vtyp (* (bound) value-type variables *)
| typ_base : vtyp (* base types *)
| typ_capt : btyp → cap → vtyp (* boxed block types *)
| typ_fvar : atom → vtyp (* (free) value-type variables *)
| typ_bvar : nat → vtyp (* (bound) value-type variables *)
Differences from the paper:
In the mechanization, we also additionally support value-type polymorphism, inherited from System F. This requires additional constructors for type variables (typ_bvar and typ_fvar), which are not present in the paper.Block Types
with btyp : Type :=
| typ_vfun : vtyp → vtyp → btyp (* function types with value arguments *)
| typ_bfun : btyp → vtyp → btyp (* function types with tracked block arguments *)
| typ_tfun : btyp → btyp (* type abstractions *)
| typ_eff : vtyp → vtyp → btyp (* capability types *)
.
| typ_vfun : vtyp → vtyp → btyp (* function types with value arguments *)
| typ_bfun : btyp → vtyp → btyp (* function types with tracked block arguments *)
| typ_tfun : btyp → btyp (* type abstractions *)
| typ_eff : vtyp → vtyp → btyp (* capability types *)
.
Differences from the paper:
In the paper, we formalize multi-arity function types. This is awkward to work with in Coq so here we only mechanize single arity function types.Syntax of Terms

Expressions
Inductive exp : Type :=
| exp_bvar : nat → exp (* (bound) expression variables *)
| exp_fvar : atom → exp (* (free) expression variables *)
| exp_const : exp (* primitives *)
| exp_box : cap → blk → exp (* box introduction *)
| exp_bvar : nat → exp (* (bound) expression variables *)
| exp_fvar : atom → exp (* (free) expression variables *)
| exp_const : exp (* primitives *)
| exp_box : cap → blk → exp (* box introduction *)
Differences from the paper:
Expressions are formalized with only one primitive value, exp_const.Statements
with stm : Type :=
| stm_ret : exp → stm (* returning *)
| stm_val : vtyp → stm → stm → stm (* sequencing *)
| stm_def : cap → btyp → blk → stm → stm (* block definition *)
| stm_vapp : blk → exp → stm (* block application (to value arguments) *)
| stm_bapp : blk → cap → blk → stm (* block application (to block arguments) *)
| stm_try : cap → vtyp → vtyp → stm → stm → stm (* handlers *)
| stm_perform : blk → exp → stm (* performing an effect *)
| stm_reset : label → cap → stm → stm → stm (* runtime delimiter *)
| stm_ret : exp → stm (* returning *)
| stm_val : vtyp → stm → stm → stm (* sequencing *)
| stm_def : cap → btyp → blk → stm → stm (* block definition *)
| stm_vapp : blk → exp → stm (* block application (to value arguments) *)
| stm_bapp : blk → cap → blk → stm (* block application (to block arguments) *)
| stm_try : cap → vtyp → vtyp → stm → stm → stm (* handlers *)
| stm_perform : blk → exp → stm (* performing an effect *)
| stm_reset : label → cap → stm → stm → stm (* runtime delimiter *)
Differences from the paper:
Similar to the syntax of types, in the mechanization we have two different forms of application (instead of multi-arity). stm_vapp takes the block to call and an expression (value argument), while stm_bapp takes the block to call, a capture annotation (to avoid implementing capture inference in the mechanization), and a block argument.Blocks
with blk : Type :=
| blk_bvar : nat → blk (* (bound) block variables *)
| blk_fvar : atom → blk (* (free) block variables *)
| blk_vabs : vtyp → stm → blk (* block implementation (with value argument) *)
| blk_babs : btyp → stm → blk (* block implementation (with block argument) *)
| blk_unbox : exp → blk (* box elimination *)
| blk_tabs : blk → blk (* value type abstraction *)
| blk_tapp : blk → vtyp → blk (* value type application *)
| blk_handler : label → blk (* runtime capability *)
.
| blk_bvar : nat → blk (* (bound) block variables *)
| blk_fvar : atom → blk (* (free) block variables *)
| blk_vabs : vtyp → stm → blk (* block implementation (with value argument) *)
| blk_babs : btyp → stm → blk (* block implementation (with block argument) *)
| blk_unbox : exp → blk (* box elimination *)
| blk_tabs : blk → blk (* value type abstraction *)
| blk_tapp : blk → vtyp → blk (* value type application *)
| blk_handler : label → blk (* runtime capability *)
.
Differences from the paper:
Again, as for statements and block types, we have two different forms of abstraction. blk_vabs to abstract over values and blk_babs to abstract over (tracked) blocks.Environments and Signatures
Environments
Like in the paper, we use a single environment for value, block, and type abstraction. We formalize environments by representing them as association lists (lists of pairs of keys and values) whose keys are atoms.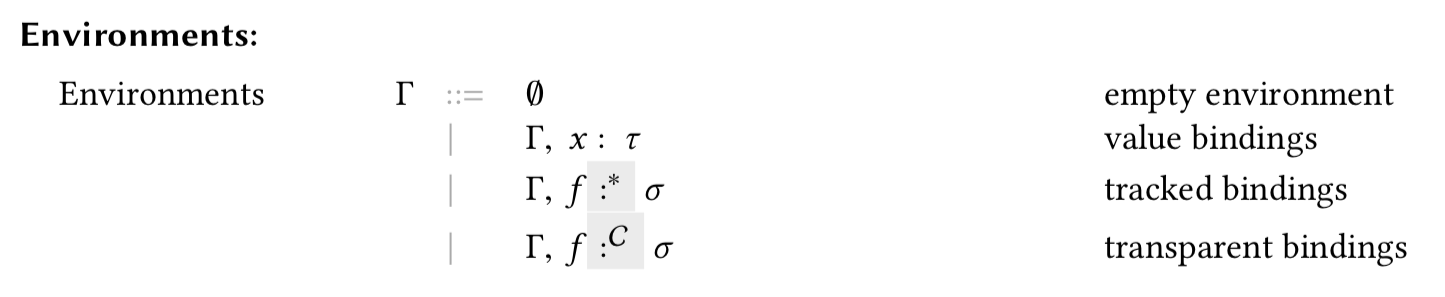
Basing our mechanization on an existing locally nameless proof, we reuse the infrastructure for environments. Util.Metatheory, Util.Environment, and Util.Signatures libraries provide functions, predicates, tactics, notations and lemmas that simplify working with environments. The Util.Environment library treats environments as lists of type list (atom × A). Since environments map atoms, the type A should encode whether a particular binding is a typing or region assumption. Thus, we instantiate A with the type binding, defined below
Inductive binding : Type :=
(* x : T *)
| bind_val : vtyp → binding
| bind_blk : btyp → coeffect → binding
(* X *)
| bind_typ : binding.
Notation env := (list (atom × binding)).
Notation empty := (@nil (atom × binding)).
Signatures
As a proof device, each runtime label (Figure 3 in the paper) is associated with a signature (that is the argument type and the result type of an effect operation).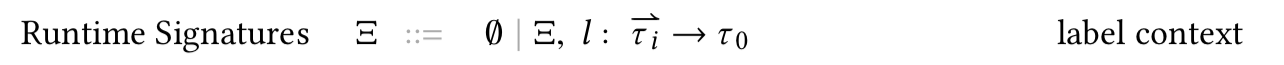
Inductive signature : Type :=
(* label : T1 (param type) T (result type)*)
| bind_sig : vtyp → vtyp → signature.
Notation sig := (list (label × signature)).
Typing
Notation "C |= D" := (cset_subset_prop D C) (at level 68).
Reserved Notation "E ; Q |-exp e ~: T" (at level 70, Q at next level).
Reserved Notation "E @ R ; Q |-blk b ~: S" (at level 70, R at next level, Q at next level).
Reserved Notation "E @ R ; Q |-stm s ~: T" (at level 70, R at next level, Q at next level).
Reserved Notation "E ; Q |-exp e ~: T" (at level 70, Q at next level).
Reserved Notation "E @ R ; Q |-blk b ~: S" (at level 70, R at next level, Q at next level).
Reserved Notation "E @ R ; Q |-stm s ~: T" (at level 70, R at next level, Q at next level).
Note on presentation: we use Gamma for E, and Xi for Q, both in the paper and in coqdoc. 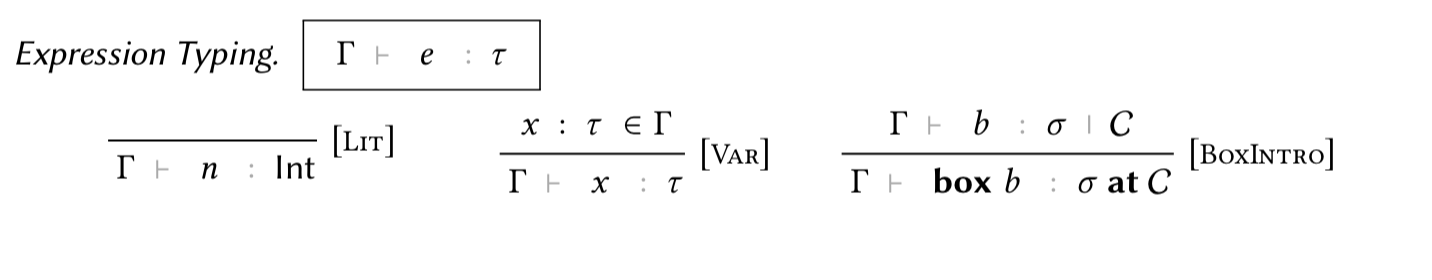
Expression Typing
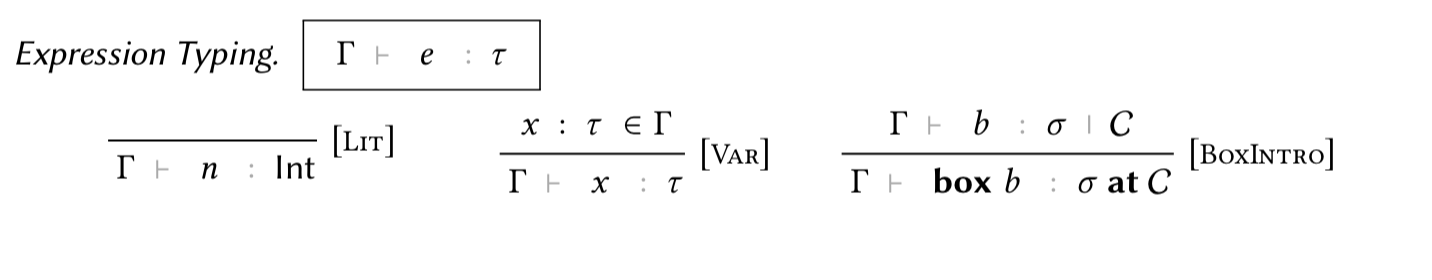
Inductive etyping : env → sig → exp → vtyp → Prop :=
| typing_base : ∀ E Q,
wf_env E →
wf_sig Q →
E ; Q |-exp exp_const ~: typ_base
| typing_evar : ∀ E Q x T,
wf_env E →
wf_sig Q →
binds x (bind_val T) E →
E ; Q |-exp (exp_fvar x) ~: T
| typing_box : ∀ E Q (C : cap) S1 b,
wf_cap E C →
(E @ C ; Q |-blk b ~: S1) →
E ; Q |-exp (exp_box C b) ~: (typ_capt S1 C)
where "E ; Q |-exp e ~: T" := (etyping E Q e T)
| typing_base : ∀ E Q,
wf_env E →
wf_sig Q →
E ; Q |-exp exp_const ~: typ_base
| typing_evar : ∀ E Q x T,
wf_env E →
wf_sig Q →
binds x (bind_val T) E →
E ; Q |-exp (exp_fvar x) ~: T
| typing_box : ∀ E Q (C : cap) S1 b,
wf_cap E C →
(E @ C ; Q |-blk b ~: S1) →
E ; Q |-exp (exp_box C b) ~: (typ_capt S1 C)
where "E ; Q |-exp e ~: T" := (etyping E Q e T)
Differences from the paper:
The three rules directly correspond to rules LIT, VAR, and BOXINTRO in the paper. As can be seen (all) typing judgements in Coq make wellformedness conditions explicit, which are left implicit in the paper.Block Typing

with btyping : env → cap → sig → blk → btyp → Prop :=
| typing_bvar_tracked : ∀ E R Q f S1,
wf_env E →
wf_sig Q →
wf_cap E R →
binds f (bind_blk S1 tracked) E →
R |= cset_fvar f →
E @ R ; Q |-blk (blk_fvar f) ~: S1
| typing_bvar_capture : ∀ E R Q f S1 (C : cap),
wf_env E →
wf_sig Q →
wf_cap E R →
R |= C →
binds f (bind_blk S1 (capture C)) E →
E @ R ; Q |-blk (blk_fvar f) ~: S1
| typing_unbox : ∀ E R Q e S1 C,
E ; Q |-exp e ~: (typ_capt S1 C) →
wf_cap E R →
R |= C →
E @ R ; Q |-blk (blk_unbox e) ~: S1
| typing_vabs : ∀ L E R Q T1 s T2,
(∀ x : atom, x `notin` L →
([(x, bind_val T1)] ++ E) @ R ; Q |-stm (open_es s x) ~: T2) →
E @ R ; Q |-blk (blk_vabs T1 s) ~: (typ_vfun T1 T2)
| typing_babs : ∀ L E R Q S1 s T2,
(∀ x : atom, x `notin` L →
([(x, bind_blk S1 tracked)] ++ E) @ cset_union R (cset_fvar x) ; Q |-stm (open_cs s x (cset_fvar x)) ~: (open_cvt T2 (cset_fvar x))) →
E @ R ; Q |-blk (blk_babs S1 s) ~: (typ_bfun S1 T2)
| typing_bvar_tracked : ∀ E R Q f S1,
wf_env E →
wf_sig Q →
wf_cap E R →
binds f (bind_blk S1 tracked) E →
R |= cset_fvar f →
E @ R ; Q |-blk (blk_fvar f) ~: S1
| typing_bvar_capture : ∀ E R Q f S1 (C : cap),
wf_env E →
wf_sig Q →
wf_cap E R →
R |= C →
binds f (bind_blk S1 (capture C)) E →
E @ R ; Q |-blk (blk_fvar f) ~: S1
| typing_unbox : ∀ E R Q e S1 C,
E ; Q |-exp e ~: (typ_capt S1 C) →
wf_cap E R →
R |= C →
E @ R ; Q |-blk (blk_unbox e) ~: S1
| typing_vabs : ∀ L E R Q T1 s T2,
(∀ x : atom, x `notin` L →
([(x, bind_val T1)] ++ E) @ R ; Q |-stm (open_es s x) ~: T2) →
E @ R ; Q |-blk (blk_vabs T1 s) ~: (typ_vfun T1 T2)
| typing_babs : ∀ L E R Q S1 s T2,
(∀ x : atom, x `notin` L →
([(x, bind_blk S1 tracked)] ++ E) @ cset_union R (cset_fvar x) ; Q |-stm (open_cs s x (cset_fvar x)) ~: (open_cvt T2 (cset_fvar x))) →
E @ R ; Q |-blk (blk_babs S1 s) ~: (typ_bfun S1 T2)
Differences from the paper:
Note that we build in subsumption on blocks (rule BSUB in the paper) into the rules as additional premises, instead of having one additional rule. This allows us to omit having to prove inversion of subeffecting.- TRACKED maps to typing_bvar_tracked
- TRANSPARENT maps to typing_bvar_capture
- BLOCK maps to typing_vabs and typing_babs
- BOXELIM maps to typing_unbox
Additional Rules for Type Polymorphism
| typing_tabs : ∀ L E R Q s T,
(∀ X : atom, X `notin` L →
([(X, bind_typ)] ++ E) @ R ; Q |-blk (open_tb s X) ~: (open_tbt T X)) →
E @ R ; Q |-blk (blk_tabs s) ~: (typ_tfun T)
| typing_tapp : ∀ E R Q s T T1,
wf_vtyp E T1 →
E @ R ; Q |-blk s ~: (typ_tfun T) →
E @ R ; Q |-blk (blk_tapp s T1) ~: (open_tbt T T1)
| typing_handler : ∀ E R Q l T1 T,
wf_env E →
wf_sig Q →
wf_cap E R →
wf_vtyp E T →
(* We are allowed to use l: *)
cset_references_lvar l R →
(* It has the correct type *)
Signatures.binds l (bind_sig T1 T) Q →
E @ R ; Q |-blk blk_handler l ~: (typ_eff T1 T)
where "E @ R ; Q |-blk b ~: S" := (btyping E R Q b S)
with styping : env → cap → sig → stm → vtyp → Prop :=
| typing_ret : ∀ E R Q e T,
E ; Q |-exp e ~: T →
wf_cap E R →
E @ R ; Q |-stm (stm_ret e) ~: T
| typing_val : ∀ L E R Q b s T1 T2,
E @ R ; Q |-stm b ~: T1 →
(∀ x : atom, x `notin` L →
([(x, bind_val T1)] ++ E) @ R ; Q |-stm (open_es s x) ~: T2) →
E @ R ; Q |-stm (stm_val T1 b s) ~: T2
| typing_def : ∀ L E R Q b s (C : cap) S1 T2,
wf_cap E C →
E @ C ; Q |-blk b ~: S1 →
(* This is a transparent binding (not tracked), we do not open types. *)
(∀ x : atom, x `notin` L →
([(x, bind_blk S1 (capture C))] ++ E) @ R ; Q |-stm (open_bs s x) ~: T2) →
E @ R ; Q |-stm (stm_def C S1 b s) ~: T2
| typing_vapp : ∀ E R Q b e T1 T2,
E @ R ; Q |-blk b ~: (typ_vfun T1 T2) →
E ; Q |-exp e ~: T1 →
E @ R ; Q |-stm (stm_vapp b e) ~: T2
| typing_bapp : ∀ E R Q b1 b2 (C : cap) S1 T2,
R |= C →
wf_cap E C →
E @ R ; Q |-blk b1 ~: (typ_bfun S1 T2) →
E @ C ; Q |-blk b2 ~: S1 →
E @ R ; Q |-stm (stm_bapp b1 C b2) ~: (open_cvt T2 C)
| typing_ret : ∀ E R Q e T,
E ; Q |-exp e ~: T →
wf_cap E R →
E @ R ; Q |-stm (stm_ret e) ~: T
| typing_val : ∀ L E R Q b s T1 T2,
E @ R ; Q |-stm b ~: T1 →
(∀ x : atom, x `notin` L →
([(x, bind_val T1)] ++ E) @ R ; Q |-stm (open_es s x) ~: T2) →
E @ R ; Q |-stm (stm_val T1 b s) ~: T2
| typing_def : ∀ L E R Q b s (C : cap) S1 T2,
wf_cap E C →
E @ C ; Q |-blk b ~: S1 →
(* This is a transparent binding (not tracked), we do not open types. *)
(∀ x : atom, x `notin` L →
([(x, bind_blk S1 (capture C))] ++ E) @ R ; Q |-stm (open_bs s x) ~: T2) →
E @ R ; Q |-stm (stm_def C S1 b s) ~: T2
| typing_vapp : ∀ E R Q b e T1 T2,
E @ R ; Q |-blk b ~: (typ_vfun T1 T2) →
E ; Q |-exp e ~: T1 →
E @ R ; Q |-stm (stm_vapp b e) ~: T2
| typing_bapp : ∀ E R Q b1 b2 (C : cap) S1 T2,
R |= C →
wf_cap E C →
E @ R ; Q |-blk b1 ~: (typ_bfun S1 T2) →
E @ C ; Q |-blk b2 ~: S1 →
E @ R ; Q |-stm (stm_bapp b1 C b2) ~: (open_cvt T2 C)
Differences from the paper:
The rules correspond to the paper with the following mapping:- RET maps to typing_ret
- VAL maps to typing_val
- DEF maps to typing_def
- APP maps to typing_vapp and typing_bapp In rule typing_val, for simplicity we do not compute the union, but instead require both restrictions to be the same. This does not affect expressivity, since we can always use subsumption.
Typing Handling of Effects
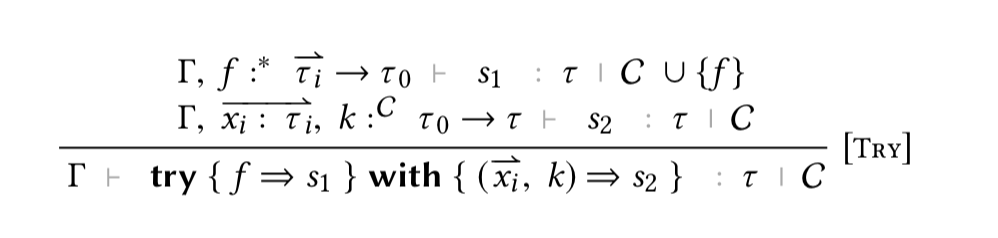
| typing_try : ∀ L E R Q C b h T T1 T2,
R |= C →
wf_cap E C →
wf_cap E R →
(* E, f : (Exc @ {*}) @ C union f |- h : T *)
(∀ f : atom, f `notin` L →
([(f, bind_blk (typ_eff T2 T1) tracked)] ++ E) @ (cset_union C (cset_fvar f)) ; Q
|-stm (open_cs b f (cset_fvar f)) ~: T) →
(* E, x : T1, k : (T2 -> T @ C) @ C |- h : T *)
(∀ (v : atom), v `notin` L →
(∀ (f : atom), f `notin` (L `union` singleton v) →
([(f, bind_blk (typ_vfun T1 T) (capture C))] ++
[(v, bind_val T2)] ++ E) @ C ; Q
|-stm (open_bs (open_es h v) f) ~: T)) →
E @ R ; Q |-stm (stm_try C T2 T1 b h) ~: T
R |= C →
wf_cap E C →
wf_cap E R →
(* E, f : (Exc @ {*}) @ C union f |- h : T *)
(∀ f : atom, f `notin` L →
([(f, bind_blk (typ_eff T2 T1) tracked)] ++ E) @ (cset_union C (cset_fvar f)) ; Q
|-stm (open_cs b f (cset_fvar f)) ~: T) →
(* E, x : T1, k : (T2 -> T @ C) @ C |- h : T *)
(∀ (v : atom), v `notin` L →
(∀ (f : atom), f `notin` (L `union` singleton v) →
([(f, bind_blk (typ_vfun T1 T) (capture C))] ++
[(v, bind_val T2)] ++ E) @ C ; Q
|-stm (open_bs (open_es h v) f) ~: T)) →
E @ R ; Q |-stm (stm_try C T2 T1 b h) ~: T
Differences from the paper:
As mentioned above, handling statements are annotated with a capture set C. Also, we use the special type constructor typ_eff instead of a function type. Otherwise, the definition is a straightforward translation to Coq in locally nameless.| typing_reset : ∀ L E R Q C l b h T T1 T2,
R |= C →
wf_cap E C →
wf_cap E R →
(* We require that the signature of l matches the type at the reset. *)
Signatures.binds l (bind_sig T2 T1) Q →
E @ (cset_union C (cset_lvar l)) ; Q |-stm b ~: T →
(∀ v : atom, v `notin` L →
(∀ f : atom, f `notin` (L `union` singleton v) →
([(f, bind_blk (typ_vfun T1 T) (capture C))] ++
[(v, bind_val T2)] ++ E) @ C ; Q
|-stm (open_bs (open_es h v) f) ~: T)) →
E @ R ; Q |-stm (stm_reset l C b h) ~: T
| typing_throw : ∀ E R Q b e T T1,
E @ R ; Q |-blk b ~: (typ_eff T1 T) →
E ; Q |-exp e ~: T1 →
E @ R ; Q |-stm (stm_perform b e) ~: T
where "E @ R ; Q |-stm s ~: T" := (styping E R Q s T).
Since we use locally nameless, the definition of typing uses the binds relation from the Environment library (in the typing_var case) and cofinite quantification in the cases involving binders (e.g., typing_vabs, typing_tabs, ...). We have to define our own induction scheme to convince the termination checker
Scheme etyping_mutind := Induction for etyping Sort Prop
with styping_mutind := Induction for styping Sort Prop
with btyping_mutind := Induction for btyping Sort Prop.
Operational Semantics
Values
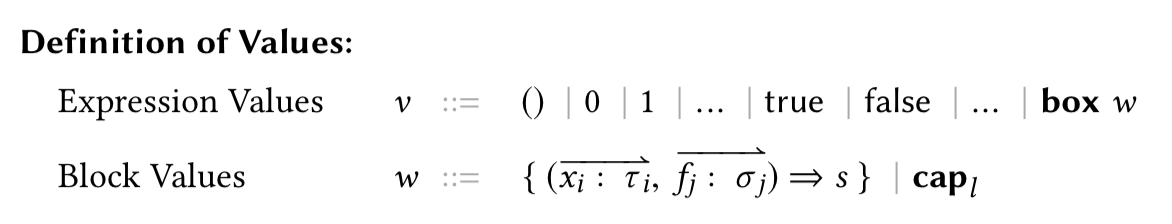
Inductive evalue : exp → Prop :=
| value_const :
evalue exp_const
| value_box : ∀ C b,
bvalue b →
capt C →
evalue (exp_box C b)
with bvalue : blk → Prop :=
| value_vfun : ∀ T s,
block (blk_vabs T s) →
bvalue (blk_vabs T s)
| value_bfun : ∀ S1 s,
block (blk_babs S1 s) →
bvalue (blk_babs S1 s)
| value_tfun : ∀ s,
block (blk_tabs s) →
bvalue (blk_tabs s)
| value_handler : ∀ l,
bvalue (blk_handler l).
Machine Redexes
Inductive machine_redex : stm → Prop :=
| redex_ret : ∀ e,
evalue e →
machine_redex (stm_ret e)
| redex_val : ∀ T b s,
machine_redex (stm_val T b s)
| redex_try : ∀ C T1 T b s,
machine_redex (stm_try C T1 T b s)
| redex_reset : ∀ l C b s,
machine_redex (stm_reset l C b s)
| redex_throw : ∀ l e,
evalue e →
machine_redex (stm_perform (blk_handler l) e).
Reserved Notation "e1 -->b e2" (at level 69).
Reserved Notation "e1 -->e e2" (at level 69).
Reserved Notation "e1 -->s e2" (at level 69).
Reduction of Blocks
Blocks can always be reduced regardless of the context. In fact, the only reduction is box-unbox elimination (bred_box) and block substitution (bred_box). Inductive bred : blk → blk → Prop :=
| bred_box : ∀ C b,
blk_unbox (exp_box C b) -->b b
| bred_tapp_cong : ∀ b b' T,
b -->b b' →
blk_tapp b T -->b blk_tapp b' T
| bred_tapp : ∀ s T,
blk_tapp (blk_tabs s) T -->b (open_tb s T)
where "b1 -->b b2" := (bred b1 b2).
| bred_box : ∀ C b,
blk_unbox (exp_box C b) -->b b
| bred_tapp_cong : ∀ b b' T,
b -->b b' →
blk_tapp b T -->b blk_tapp b' T
| bred_tapp : ∀ s T,
blk_tapp (blk_tabs s) T -->b (open_tb s T)
where "b1 -->b b2" := (bred b1 b2).
Reduction of Expressions
Reduction on expressions is even simpler. Only boxed blocks can be reduced at all. Inductive ered : exp → exp → Prop :=
| ered_box : ∀ C b b',
b -->b b' →
(exp_box C b) -->e (exp_box C b')
where "e1 -->e e2" := (ered e1 e2).
| ered_box : ∀ C b b',
b -->b b' →
(exp_box C b) -->e (exp_box C b')
where "e1 -->e e2" := (ered e1 e2).
Inductive sred : stm → stm → Prop :=
| sred_ret : ∀ e e',
e -->e e' →
stm_ret e -->s stm_ret e'
| sred_vapp_3 : ∀ T s e,
evalue e →
stm_vapp (blk_vabs T s) e -->s (open_es s e)
| sred_ret : ∀ e e',
e -->e e' →
stm_ret e -->s stm_ret e'
| sred_vapp_3 : ∀ T s e,
evalue e →
stm_vapp (blk_vabs T s) e -->s (open_es s e)
The remaining rules are congruences, omitted in the appendix of the paper.
| sred_def_1 : ∀ C S1 b b' s,
b -->b b' →
stm_def C S1 b s -->s stm_def C S1 b' s
| sred_def_2 : ∀ C S1 b s,
bvalue b →
stm_def C S1 b s -->s (open_bs s b)
| sred_vapp_1 : ∀ b b' e,
b -->b b' →
stm_vapp b e -->s stm_vapp b' e
| sred_vapp_2 : ∀ b e e',
e -->e e' →
stm_vapp b e -->s stm_vapp b e'
| sred_bapp_1 : ∀ b1 b1' C b2,
b1 -->b b1' →
stm_bapp b1 C b2 -->s stm_bapp b1' C b2
| sred_bapp_2 : ∀ b1 C b2 b2',
b2 -->b b2' →
stm_bapp b1 C b2 -->s stm_bapp b1 C b2'
| sred_bapp_3 : ∀ S1 s C b2,
bvalue b2 →
stm_bapp (blk_babs S1 s) C b2 -->s (open_cs s b2 C)
| sred_throw_1 : ∀ b b' e,
b -->b b' →
stm_perform b e -->s stm_perform b' e
| sred_throw_2 : ∀ b e e',
bvalue b →
e -->e e' →
stm_perform b e -->s stm_perform b e'
where "b1 -->s b2" := (sred b1 b2)
.
b -->b b' →
stm_def C S1 b s -->s stm_def C S1 b' s
| sred_def_2 : ∀ C S1 b s,
bvalue b →
stm_def C S1 b s -->s (open_bs s b)
| sred_vapp_1 : ∀ b b' e,
b -->b b' →
stm_vapp b e -->s stm_vapp b' e
| sred_vapp_2 : ∀ b e e',
e -->e e' →
stm_vapp b e -->s stm_vapp b e'
| sred_bapp_1 : ∀ b1 b1' C b2,
b1 -->b b1' →
stm_bapp b1 C b2 -->s stm_bapp b1' C b2
| sred_bapp_2 : ∀ b1 C b2 b2',
b2 -->b b2' →
stm_bapp b1 C b2 -->s stm_bapp b1 C b2'
| sred_bapp_3 : ∀ S1 s C b2,
bvalue b2 →
stm_bapp (blk_babs S1 s) C b2 -->s (open_cs s b2 C)
| sred_throw_1 : ∀ b b' e,
b -->b b' →
stm_perform b e -->s stm_perform b' e
| sred_throw_2 : ∀ b e e',
bvalue b →
e -->e e' →
stm_perform b e -->s stm_perform b e'
where "b1 -->s b2" := (sred b1 b2)
.
Inductive frame : Type :=
(* val _ : T = ; s *)
| K : vtyp → stm → frame
(* invariant: all elements in cap are bound in the tail of the ctx *)
| H : label → cap → stm → frame
.
We use the following abbreviation to denote runtime stacks
The toplevel / empty runtime stack.
The following definition extracts labels, bound by the context.
Fixpoint bound_labels (c : ctx) : labels :=
match c with
| nil ⇒ {}L
| K T s :: c ⇒ bound_labels c
| H l C h :: c ⇒ LabelSet.F.union (bound_labels c) (LabelSet.F.singleton l)
end.
match c with
| nil ⇒ {}L
| K T s :: c ⇒ bound_labels c
| H l C h :: c ⇒ LabelSet.F.union (bound_labels c) (LabelSet.F.singleton l)
end.
We need to be able to plug an expression into a context.
Fixpoint plug (c : ctx) (e : exp) {struct c} : stm :=
match c with
| nil ⇒ stm_ret e
| K T s :: c ⇒ stm_val T (plug c e) s
| H l C h :: c ⇒ stm_reset l C (plug c e) h
end.
Reserved Notation "R ; Q |-cnt k ~: T1 ~> T2" (at level 70, Q at next level).
Reserved Notation "R ; Q |-ctx c ~: T" (at level 70, Q at next level).
match c with
| nil ⇒ stm_ret e
| K T s :: c ⇒ stm_val T (plug c e) s
| H l C h :: c ⇒ stm_reset l C (plug c e) h
end.
Reserved Notation "R ; Q |-cnt k ~: T1 ~> T2" (at level 70, Q at next level).
Reserved Notation "R ; Q |-ctx c ~: T" (at level 70, Q at next level).
Context typing
The following definition models the context typing from Appendix A.3 in the paper.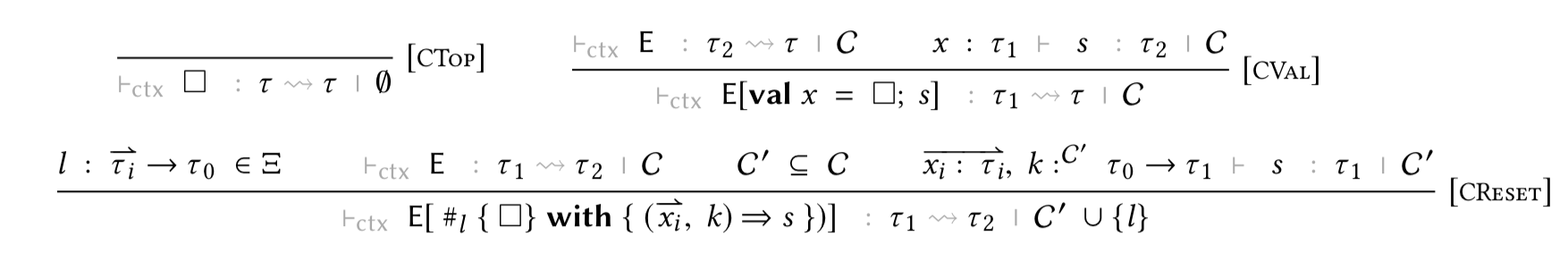
Inductive typing_ctx : cap → sig → ctx → vtyp → Prop :=
| typing_ctx_empty : ∀ Q T,
wf_sig Q →
empty_cset ; Q |-ctx top ~: T
| typing_ctx_frame : ∀ L R Q c T1 T2 s,
R ; Q |-ctx c ~: T2 →
(∀ X : atom, X `notin` L →
[(X, bind_val T1)] @ R ; Q |-stm (open_es s X) ~: T2) →
R ; Q |-ctx K T1 s :: c ~: T1
| typing_ctx_try : ∀ L R Q l C c T T1 T2 s,
R ; Q |-ctx c ~: T →
R |= C →
wf_cap empty C →
Signatures.binds l (bind_sig T1 T2) Q →
(∀ v : atom, v `notin` L →
(∀ f : atom, f `notin` (L `union` singleton v) →
[(f, bind_blk (typ_vfun T2 T) (capture C))] ++
[(v, bind_val T1)] @ C ; Q
|-stm (open_bs (open_es s v) f) ~: T)) →
cset_union C (cset_lvar l) ; Q |-ctx H l C s :: c ~: T
where "R ; Q |-ctx K ~: T" := (typing_ctx R Q K T).
| typing_ctx_empty : ∀ Q T,
wf_sig Q →
empty_cset ; Q |-ctx top ~: T
| typing_ctx_frame : ∀ L R Q c T1 T2 s,
R ; Q |-ctx c ~: T2 →
(∀ X : atom, X `notin` L →
[(X, bind_val T1)] @ R ; Q |-stm (open_es s X) ~: T2) →
R ; Q |-ctx K T1 s :: c ~: T1
| typing_ctx_try : ∀ L R Q l C c T T1 T2 s,
R ; Q |-ctx c ~: T →
R |= C →
wf_cap empty C →
Signatures.binds l (bind_sig T1 T2) Q →
(∀ v : atom, v `notin` L →
(∀ f : atom, f `notin` (L `union` singleton v) →
[(f, bind_blk (typ_vfun T2 T) (capture C))] ++
[(v, bind_val T1)] @ C ; Q
|-stm (open_bs (open_es s v) f) ~: T)) →
cset_union C (cset_lvar l) ; Q |-ctx H l C s :: c ~: T
where "R ; Q |-ctx K ~: T" := (typing_ctx R Q K T).
Continuation typing
Continuations are reversed contexts, so the typing rules are very similar. The rendering R ; Q |-cnt K ~: T1 ~> T2 shows that continuations K have a function-like type. The hole has type T1 and they are delimited at T2. Inductive typing_cnt : cap → sig → ctx → vtyp → vtyp → Prop :=
| typing_cnt_empty : ∀ R Q T,
wf_cap empty R →
wf_sig Q →
R ; Q |-cnt top ~: T ~> T
| typing_cnt_frame : ∀ L R Q c T1 T2 T3 s,
R ; Q |-cnt c ~: T1 ~> T2 →
(∀ X : atom, X `notin` L →
[(X, bind_val T2)] @ R ; Q |-stm (open_es s X) ~: T3) →
R ; Q |-cnt K T2 s :: c ~: T1 ~> T3
| typing_cnt_handler : ∀ L R Q c l C T T1 T2 T3 h,
wf_cap empty R →
cset_union C (cset_lvar l) ; Q |-cnt c ~: T1 ~> T2 →
R |= C →
Signatures.binds l (bind_sig T3 T) Q →
(∀ v : atom, v `notin` L →
(∀ f : atom, f `notin` (L `union` singleton v) →
[(f, bind_blk (typ_vfun T T2) (capture C))] ++
[(v, bind_val T3)] @ C ; Q |-stm (open_bs (open_es h v) f) ~: T2)) →
R ; Q |-cnt (H l C h :: c) ~: T1 ~> T2
where "R ; Q |-cnt K ~: T1 ~> T2" := (typing_cnt R Q K T1 T2).
| typing_cnt_empty : ∀ R Q T,
wf_cap empty R →
wf_sig Q →
R ; Q |-cnt top ~: T ~> T
| typing_cnt_frame : ∀ L R Q c T1 T2 T3 s,
R ; Q |-cnt c ~: T1 ~> T2 →
(∀ X : atom, X `notin` L →
[(X, bind_val T2)] @ R ; Q |-stm (open_es s X) ~: T3) →
R ; Q |-cnt K T2 s :: c ~: T1 ~> T3
| typing_cnt_handler : ∀ L R Q c l C T T1 T2 T3 h,
wf_cap empty R →
cset_union C (cset_lvar l) ; Q |-cnt c ~: T1 ~> T2 →
R |= C →
Signatures.binds l (bind_sig T3 T) Q →
(∀ v : atom, v `notin` L →
(∀ f : atom, f `notin` (L `union` singleton v) →
[(f, bind_blk (typ_vfun T T2) (capture C))] ++
[(v, bind_val T3)] @ C ; Q |-stm (open_bs (open_es h v) f) ~: T2)) →
R ; Q |-cnt (H l C h :: c) ~: T1 ~> T2
where "R ; Q |-cnt K ~: T1 ~> T2" := (typing_cnt R Q K T1 T2).
Abstract Machine
- either we simply step within a context state_step,
- or we unwind the stack to search for a delimiter state_wind.
Inductive state : Type :=
| state_step (s : stm) (c : ctx) (Q : sig) : state
| state_wind (l : label) (v : exp) (c : ctx) (k : ctx) (Q : sig) : state
.
Notation "〈throw l # v | c • k | Q 〉" := (state_wind l v c k Q).
Notation "〈 s | c | Q 〉" := (state_step s c Q).
Notation "〈 e | Q 〉" := (state_step (stm_ret e) top Q).
Reserved Notation "st1 --> st2" (at level 69).
| state_step (s : stm) (c : ctx) (Q : sig) : state
| state_wind (l : label) (v : exp) (c : ctx) (k : ctx) (Q : sig) : state
.
Notation "〈throw l # v | c • k | Q 〉" := (state_wind l v c k Q).
Notation "〈 s | c | Q 〉" := (state_step s c Q).
Notation "〈 e | Q 〉" := (state_step (stm_ret e) top Q).
Reserved Notation "st1 --> st2" (at level 69).
The following predicate corresponds to values, but for machine states.
(cong)
(pop)
(ret)
(push)
| step_push : ∀ Q s T b c,
stmt (stm_val T b s) →
〈 stm_val T b s | c | Q 〉 --> 〈 b | K T s :: c | Q 〉
stmt (stm_val T b s) →
〈 stm_val T b s | c | Q 〉 --> 〈 b | K T s :: c | Q 〉
(try)
| step_try : ∀ Q s h l C T2 T1 c,
¬ LabelSet.F.In l (bound_labels c) →
¬ LabelSet.F.In l (Signatures.dom Q) →
〈 stm_try C T2 T1 s h | c | Q 〉-->
〈 open_cs s (blk_handler l) (cset_lvar l) | H l C h :: c | [(l , bind_sig T2 T1)] ++ Q 〉
¬ LabelSet.F.In l (bound_labels c) →
¬ LabelSet.F.In l (Signatures.dom Q) →
〈 stm_try C T2 T1 s h | c | Q 〉-->
〈 open_cs s (blk_handler l) (cset_lvar l) | H l C h :: c | [(l , bind_sig T2 T1)] ++ Q 〉
(reset)
| step_reset : ∀ Q s h l C T1 T c,
Signatures.binds l (bind_sig T1 T) Q →
〈 stm_reset l C s h | c | Q 〉--> 〈 s | H l C h :: c | Q 〉
Signatures.binds l (bind_sig T1 T) Q →
〈 stm_reset l C s h | c | Q 〉--> 〈 s | H l C h :: c | Q 〉
(try), switch to search mode
| step_throw : ∀ Q l v c,
evalue v →
〈 stm_perform (blk_handler l) v | c | Q 〉-->
〈throw l # v | c • top | Q 〉
evalue v →
〈 stm_perform (blk_handler l) v | c | Q 〉-->
〈throw l # v | c • top | Q 〉
(unwind)
| step_unwind_1 : ∀ Q l v T s c k,
〈throw l # v | K T s :: c • k | Q 〉--> 〈throw l # v | c • K T s :: k | Q 〉
〈throw l # v | K T s :: c • k | Q 〉--> 〈throw l # v | c • K T s :: k | Q 〉
(forward)
| step_unwind_2 : ∀ Q l v l2 C h c k,
l ≠ l2 →
〈throw l # v | H l2 C h :: c • k | Q 〉--> 〈throw l # v | c • H l2 C h :: k | Q 〉
l ≠ l2 →
〈throw l # v | H l2 C h :: c • k | Q 〉--> 〈throw l # v | c • H l2 C h :: k | Q 〉
(handle), switch back to step mode
| step_handle : ∀ Q l v T T1 C h c k,
(* the continuation: (y : T1) => reset l c h Ey *)
Signatures.binds l (bind_sig T T1) Q →
〈throw l # v | H l C h :: c • k | Q 〉-->
〈 open_bs (open_es h v)
(blk_vabs T1 (plug (H l C h :: k) (exp_bvar 0))) | c | Q 〉
where "st1 --> st2" := (step st1 st2).
(* the continuation: (y : T1) => reset l c h Ey *)
Signatures.binds l (bind_sig T T1) Q →
〈throw l # v | H l C h :: c • k | Q 〉-->
〈 open_bs (open_es h v)
(blk_vabs T1 (plug (H l C h :: k) (exp_bvar 0))) | c | Q 〉
where "st1 --> st2" := (step st1 st2).
Abstract Machine Typing
A machine state is simply by composing the previously defined typing judgements.Inductive typing_state : state → Prop :=
| typ_step : ∀ R Q s c T,
R ; Q |-ctx c ~: T →
nil @ R ; Q |-stm s ~: T →
typing_state〈 s | c | Q 〉
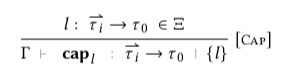 Like in the other rules, we bake subsumption into this rule.
Like in the other rules, we bake subsumption into this rule.